Shilin Liu
ComplexGen: CAD Reconstruction by B-Rep Chain Complex Generation
May 29, 2022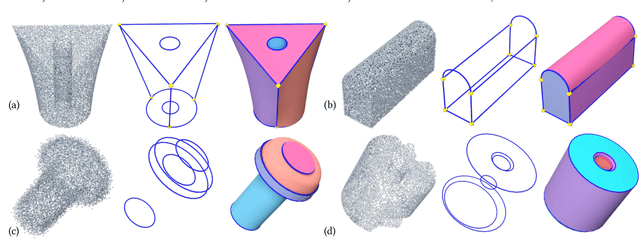

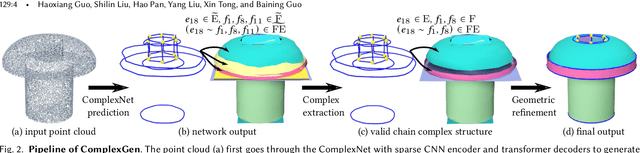

Abstract:We view the reconstruction of CAD models in the boundary representation (B-Rep) as the detection of geometric primitives of different orders, i.e. vertices, edges and surface patches, and the correspondence of primitives, which are holistically modeled as a chain complex, and show that by modeling such comprehensive structures more complete and regularized reconstructions can be achieved. We solve the complex generation problem in two steps. First, we propose a novel neural framework that consists of a sparse CNN encoder for input point cloud processing and a tri-path transformer decoder for generating geometric primitives and their mutual relationships with estimated probabilities. Second, given the probabilistic structure predicted by the neural network, we recover a definite B-Rep chain complex by solving a global optimization maximizing the likelihood under structural validness constraints and applying geometric refinements. Extensive tests on large scale CAD datasets demonstrate that the modeling of B-Rep chain complex structure enables more accurate detection for learning and more constrained reconstruction for optimization, leading to structurally more faithful and complete CAD B-Rep models than previous results.
Convolutional Neural Networks on 3D Surfaces Using Parallel Frames
Aug 15, 2018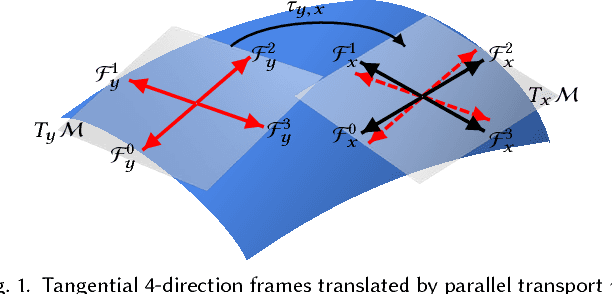
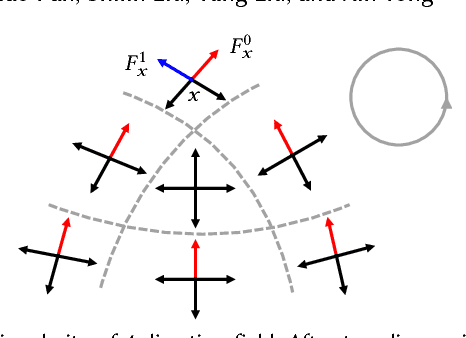
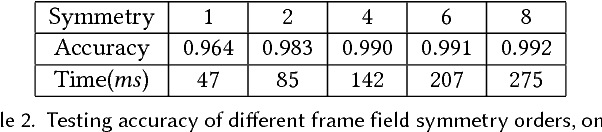

Abstract:We extend Convolutional Neural Networks (CNNs) on flat and regular domains (e.g. 2D images) to curved surfaces embedded in 3D Euclidean space that are discretized as irregular meshes and widely used to represent geometric data in Computer Vision and Graphics. We define surface convolution on tangent spaces of a surface domain, where the convolution has two desirable properties: 1) the distortion of surface domain signals is locally minimal when being projected to the tangent space, and 2) the translation equi-variance property holds locally, by aligning tangent spaces with the canonical parallel transport that preserves metric. For computation, we rely on a parallel N-direction frame field on the surface that minimizes field variation and therefore is as compatible as possible to and approximates the parallel transport. On the tangent spaces equipped with parallel frames, the computation of surface convolution becomes standard routine. The frames have rotational symmetry which we disambiguate by constructing the covering space of surface induced by the parallel frames and grouping the feature maps into N sets accordingly; convolution is computed on the N branches of the cover space with respective feature maps while the kernel weights are shared. To handle irregular points of a discrete mesh while sharing kernel weights, we make the convolution semi-discrete, i.e. the convolution kernels are polynomial functions, and their convolution with discrete surface points becomes sampling and weighted summation. Pooling and unpooling operations are computed along a mesh hierarchy built through simplification. The presented surface CNNs allow effective deep learning on meshes. We show that for tasks of classification, segmentation and non-rigid registration, surface CNNs using only raw input signals achieve superior performances than previous models using sophisticated input features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge